Prediction of Maximum Pressure in a Slider Pad Bearing using Machine Learning

Objective and Overview

This study aims at predicting the maximum pressure in a hydrodynamic plane slider pad bearing using Machine Learning.

The cost of computation of a problem is directly related to the complexity of the problem and the availability of resources to solve that. Adding to this, the time spent on solving will affect the product development cycle. Adopting Machine Learning in the domain of solving engineering problems can save significant amount of time to get an approximate result/response compared to a numerical method, provided there is a past experience on how the product was developed.

Method

In this study, Supervised Machine Learning – Linear Regression algorithm is used to train the data and predict the new response of the system.

Linear Regression is an algorithm that belongs to the class of Supervised learning in Machine Learning. This algorithm takes the data of independent and dependent variables and is trained to predict the parameters (coefficient terms) associated with the independent variables. Given a set of new independent variables, linear regression predicts the dependent variable. An optimisation technique is used to find the optimal values of these parameters. In this study, Gradient Descent is used.

Problem Definition and Solution

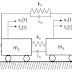
The problem considered in this case is a hydrodynamic slider pad bearing and the maximum pressure induced in it. The system is studied for different velocities and viscosities of the flow and the corresponding dataset is prepared using the finite difference method applied to Reynold’s equation. The detailed numerical modeling can be found in the previous blog.

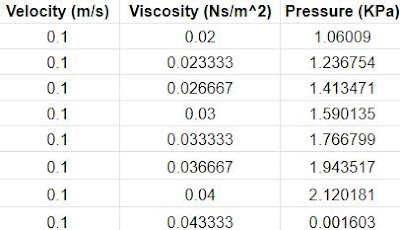
The dataset consists of 100 samples with different combinations of velocities and viscosities vectors as shown in the figure below. All the data points are shown in the representative figure.

α₁, α₂ and α₃ are considered as the intercept and the coefficient terms associated with the velocity and viscosity respectively. A hypothesis is formulated to predict the pressure with the given values in the following way.

A cost function is generated in the following way to find the error between the predicted and the actual values. Here 'm' refers to the total number of samples available in the data and 'P' refers to the actual pressure value.

The cost function is minimised using the gradient descent optimisation technique to find the optimal values of α₁, α₂ and α₃. This method starts with an initial value of a parameter and later update its value based on the learning parameter 'α' and the cost function 'J' as shown below.

Once these parameters are updated, the cost function is evaluated to determine the error. This process keeps iterating until a convergence is achieved or the difference between consecutive cost functional values is acceptable.

The cost function evaluated for various iterations of the parameters to predict the pressure in the slider pad bearing can be seen below. It can be observed that there is a good convergence of the cost function.

The optimal parameters of α₁, α₂ and α₃ are obtained as follows.

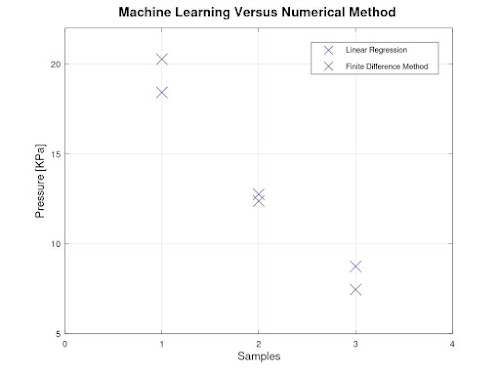
The parameters produced from Machine Learning are used to predict the pressure. The predicted values and the actual values are depicted in the figures below. 

It can be concluded that there is a good agreement between the predicted and the actual values as it can be observed from the error rate. This not only gives an approximate result but also helps to take quick and faster decision in the product development process.