Introduction
The study of modal characteristics is important to determine the natural frequencies of the system. In this study, a four DOF (degrees-of-freedom) system as shown in figure 1 is studied for the parameters tabulated in table 1. The mass, stiffness and damping matrices for the whole system are calculated and finally, the frequency response function is calculated to observe the resonant frequencies of the system.
A data set is prepared by modifying the mass and the parallel stiffness of the system for a different set of values and the respective first resonant frequencies are recorded. Latin hypercube sampling is used to optimally distribute the data points (mass & stiffness) in the design space, to prepare the data.
The data obtained is trained using KNN (k-nearest neighbors regression) by selecting an optimal value of k. The trained KNN is used to predict the resonant frequency of a new set of mass and stiffness. It was observed that the prediction is close to the actual value.
Modal Analysis
The dynamic equation of motion, global mass, stiffness and damping matrices for the 4 DOF system are derived in the following way.
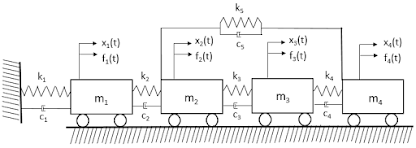 |
| Figure 1: 4 DOF System |
|
DOF number |
Mass (kg) |
Stiffness (N/m) |
|
1 |
125 |
10e6 |
|
2 |
75 |
10.2e6 |
|
3 |
45 |
21e6 |
|
4 |
15 |
9.5e6 |
|
5 |
|
5e4 |
Proportion coefficient to mass matrix, a = 0.5
Proportion coefficient to stiffness matrix, b = 0.00001
The equations of motion for each mass are derived in the following way.

Writing the mass, stiffness and damping matrices according to the following relation.
 |
| Figure 2 :Accelerance - Input at DOF4, Output at DO4 |
 |
| Figure 3: Accelerance - Input at DOF2, Output at DO2 |
 |
| Figure 4: Accelerance - Input at DOF2, Output at DO4 |
Machine Learning






No comments:
Post a Comment